Project Euler Solution 15

Problem Statement

Starting in the top left corner in a 20 by 20 grid, how many routes are there to the bottom right corner?

Starting in the top left corner of a 2×2 grid, there are 6 routes (without backtracking) to the bottom right corner.

How many routes are there through a 20×20 grid?

Solution

In a 2×2 grid, there are 3 rows and 3 columns

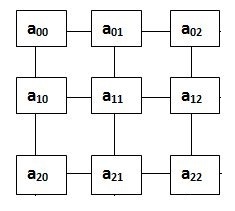
So our problem is to find the number of routes from top left corner a₀₀ to bottom right corner a₂₂. Let me show you what are the different routes that can be reached from a₀₀ to a₂₂ using a tree representation.

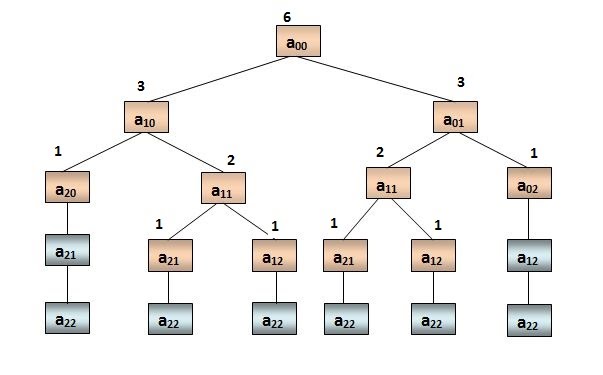
Let us denote each node in this tree as aij and number of routes from aij to the destination node as routes[i][j]. The value at the top of each node represents the total number of routes from that node to the destination.

1. Number of routes from a node aij is the sum of the routes from its left and right child. routes[i][j] = routes[i + 1][j] + routes[i][j + 1]
2. But when i=j, the number of routes from either of its child is always same. So it’s enough to find the routes from one of its child and then double it. routes[i][j] = 2 routes[i + 1][j] or routes[i][j] = 2 routes[i][j + 1]
3. When i = 2 or j = 2 (Note: 2 is the grid size), the number of routes from that node to destination is 1. So this is the terminating condition. routes[GRID_SIZE][j] = 1 routes[i][GRID_SIZE] = 1

To speed up the program I have used an array to store the routes of the node that are already found. So whenever a node for which the route is already known is encountered, just take it from the array.

Implementation

#include <stdio.h>
int GRID_SIZE = 20;long long int tree_routes[21][21] = { 0 };long long int Routes(int, int);
int main(){    long long int no_of_routes;    no_of_routes = Routes(0, 0);    printf("%lld", no_of_routes);    return 0;}
long long int Routes(int i, int j){    long long int route, route1, route2;    route = 0;    route1 = 0;    route2 = 0;    if (tree_routes[i][j] != 0)    {        route = tree_routes[i][j];        return route;    }    while (i < (GRID_SIZE + 1) && j < (GRID_SIZE + 1))    {        if (i == GRID_SIZE || j == GRID_SIZE)        {            route = 1;            tree_routes[i][j] = 1;            return route;        }        if (i == j && i != GRID_SIZE && j != GRID_SIZE)        {            if (tree_routes[i + 1][j] != 0)            {                route = 2 *tree_routes[i + 1][j];                return route;            }            else            {                route = 2* Routes(i + 1, j);                tree_routes[i][j] = route;                return route;            }        }        if (tree_routes[i + 1][j] != 0) route1 = tree_routes[i + 1][j];        else route1 = Routes(i + 1, j);        if (tree_routes[i][j + 1] != 0) route2 = tree_routes[i][j + 1];        else route2 = Routes(i, j + 1);        route = route1 + route2;        tree_routes[i][j] = route;        return route;    }}

Sample Output