Project Euler Solution 67

Problem Statement#

Using an efficient algorithm find the maximal sum in the triangle?

By starting at the top of the triangle below and moving to adjacent numbers on the row below, the maximum total from top to bottom is 23.

    3
   7 4
  2 4 6
8 5 9 3

That is, 3 + 7 + 4 + 9 = 23.

Find the maximum total from top to bottom in triangle.txt (right click and 'Save Link/Target As...'), a 15K text file containing a triangle with one-hundred rows.

NOTE: This is a much more difficult version of problem 18. It is not possible to try every route to solve this problem, as there are 2⁹⁹ altogether! If you could check one trillion (10¹²) routes every second it would take over twenty billion years to check them all. There is an efficient algorithm to solve it. ;o)

Solution#

The correct algorithm is somewhat similar to the one in problem 18, where I started from top to bottom. But here I have considered bottom to top.

Let me consider the above sample input:

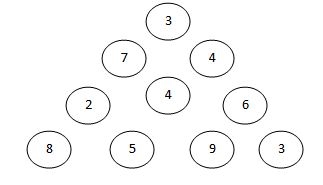
Sample Output

There are four levels, which is equal to the number of rows. Level 4 is the desination level and there are four possibilities: Like the destination may be 8 or 5 or 9 or 3.

8 and 5 are the possible routes from 2.

8 > 5, 8 + 2 = 10

5 and 9 are the possible routes from 4.

9 > 5, 9 + 4 = 13

9 and 3 are the possible routes from 6.

9 > 3, 9 + 6 = 15

Sample Output

10 and 13 are the possible routes from 7.

13 > 10, 13 + 7 = 20

13 and 15 are the possible routes from 4. 15 > 13, 15 + 4 = 19

Sample Output

20 and 19 are possible route from 3

20 > 19, 20 + 3 = 23

Sample Output

The solution is 23

This is too simple and easy to implement than what I did in problem 18. Also works for both problem 18 and 67.

Implementation#

#include <stdio.h>#include <stdlib.h>
int No_Rows = 100;
int main(){    int number[6000];    int index, level, num;    FILE * f_read;    f_read = fopen("trianglepe067.txt", "rt");    index = 0;    while (fscanf(f_read, "%d", &num) == 1)    {        number[index] = num;        index++;    }    index--;    level = No_Rows;    while (level != 1)    {        for (int i = index - (level - 1); i < index; i++)        {            if (number[i] > number[i + 1])            {                number[i - (level - 1)] = number[i - (level - 1)] + number[i];            }            else            {                number[i - (level - 1)] = number[i - (level - 1)] + number[i + 1];            }        }        index = index - level;        level--;    }    printf("%d", number[0]);    return 0;
}

Sample Output#

Sample Output