Project Euler Solution 16

Problem Statement

What is the sum of the digits of the number 2¹⁰⁰⁰?

2¹⁵ = 32768 and the sum of its digits is 3 + 2 + 7 + 6 + 8 = 26.

What is the sum of the digits of the number 2¹⁰⁰⁰?

Solution

Solution to our problem is just multiplying 2, thousand times and finding the sum of the digits in the final answer. But the answer is not small enough to fit into our data types that exist. So I have used what I have done in problem 13 to find 2¹⁰⁰⁰. Let us see, what is the sum of the digits of the number 2⁷?

This can be done by adding as follows

2⁰ = 1

2¹ = 2⁰ + 2⁰ = 1 + 1 = 2

2² = 2¹ + 2¹ = 2 + 2 = 4

2³ = 2² + 2² = 4 + 4 = 8

2⁴ = 2³ + 2³ = 8 + 8 = 16

2⁵ = 2⁴ + 2⁴ = 16 + 16 = 32

Initially number is 1 which is 2⁰ and the carry is 0.

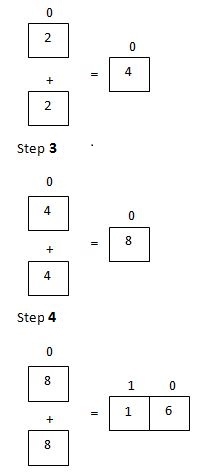
Here sum=16 which is greater than 9. So definitely there will be a carry. Insert 6 (i.e., 16%10) into the array and set and to get the carry divide the sum by 10. So the carry is 1. Since 8 is a single digit number, just insert the carry in the next position. As you see above the number is stored in reverse direction as 61(6 in position 0 and 1 in the position 1).

note

Whenever the number in the last position is greater than 4, it means than the resulting sum contains one digit more than the number. So increase the array size by 1. Here 8 is the number in the last position and is greater than 4, so the resulting sum will contain a digit one more than the previous cases.

This is a two digit number. The number in the last position i.e., in the position 1 is less than 4, so the resulting sum is also a two digit number. Each of these steps is similar to problem 13 where hundred 50 digit numbers are added (here we are adding just two 2-digit numbers).

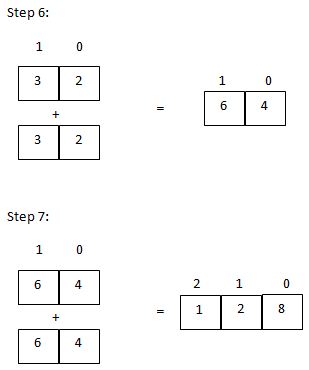
Now we have the answer for 2⁷ which is 128. So the sum of the digits is 1 + 2 + 8 = 11.

Implementation

#include <stdio.h>
int POW_SIZE = 1000;int main(){    int i, j, k, sum, carry, count, t_sum, init_digits, no_digits;    int num[1000], t_num[1000];    num[0] = 1;    count = 1;    init_digits = 1;    while (count <= POW_SIZE)    {        no_digits = init_digits;        carry = 0;        j = 0;        if (num[no_digits - 1] >= 5) no_digits++;        for (i = 0; i < no_digits; i++)        {            t_sum = num[i] + num[i] + carry;            if (t_sum < 10)            {                t_num[j] = t_sum % 10;                carry = 0;            }            if (t_sum >= 10)            {                t_num[j] = t_sum % 10;                t_sum = t_sum / 10;                carry = t_sum % 10;            }            j++;            if (j == no_digits) break;        }        init_digits = no_digits;        sum = 0;        for (k = 0; k < no_digits; k++)        {            num[k] = t_num[k];            sum = sum + num[k];        }        count++;    }    printf("%d", sum);    return 0;}

Sample Output